今天大概看了看傅立叶级数。书中介绍的 半幅 傅里叶级数有两种,第一种是 $\sum\limits_{n=1}^\infty c_n \sin\frac{n\pi x}{L}$, 一般用于展开奇函数;另一种是 $d_0 + \sum\limits_{n=1}^\infty d_n \cos\frac{n\pi x}{L}$, 一般用于展开偶函数。 看到此时,突发奇想,如果将 $\cos x,\ x \in (0,\pi)$ 强行用第一种方式(只含 $\sin$ 函数)展开,结果会如何呢?
维基上查了一下,发现正好有此例子,决定作图看看,正好趁此机会复习一下 Mathematica. 作图过程中无意间发现 Mathematica 竟然可以直接导出 gif 文件,折腾许久,终于有如下结果:
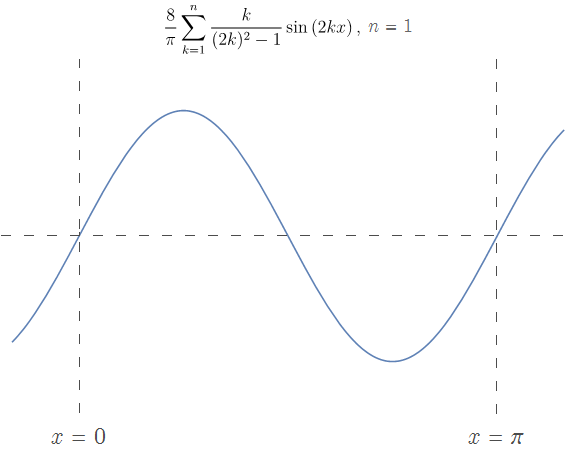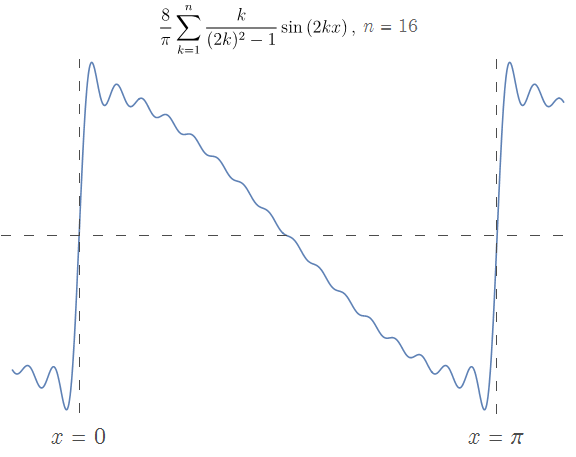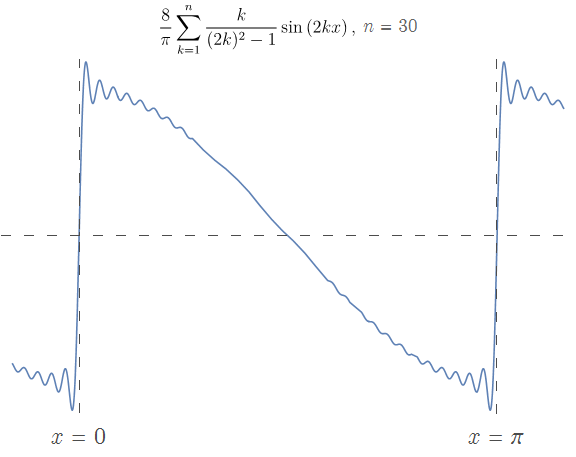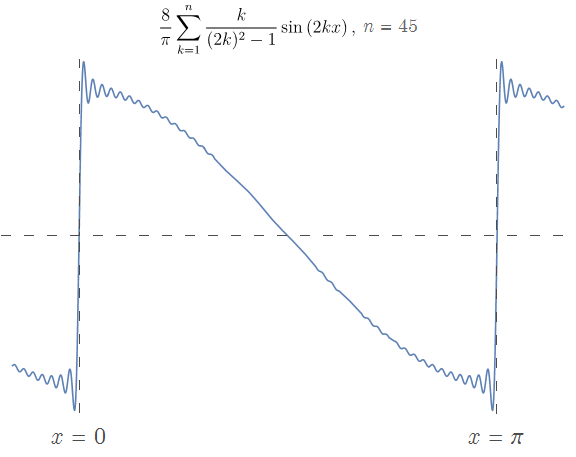
$n < \infty$ 时的函数图像经过原点,同时又要逼近轴上的 $y = 1$ 点, 因此在 $x=0$ 附近近乎于直线上升。可见如果没有:
\[\lim\limits_{x \rightarrow 0^+} f(x) = 0\]对 $f(x),\ x \in (0,L)$ 使用 $\sin$ 函数半幅傅里叶展开,大概不是一个明智的选择;尤其是在 $x=0$ 附近,效果堪忧。
2018-02-19: 经 @不是灵魂画师 提醒,数学意义上(technically)展开式是收敛的,只是收敛到奇延拓的 $\cos x$. 可见关键并不在于收敛与否,而是收敛结果是否具有间断。往往,间断点附近的截断展开式具有较为恶劣的行为(不能良好地反映原函数,此处即 $\cos x$. )
P.S. 贴上自己写的略显啰嗦的 Mathematica 代码;图中的 TeX 标签通过 MaTeX 扩展实现。